Fluid-structure interactions in viscoelastic fluids
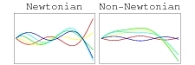
For eukaryotic flagella, swimming results from an interplay of hydrodynamic forces and flagellar forces. The altered hydrodynamic forces in a viscoelastic fluid can change the beating patterns of flagella. These shape changes are as important as nonlinear viscoelastic effects in determining swimming properties. (Published in Phys. Rev. Lett. [pdf] and Phys. Rev. E. [pdf] Right image captions: Sperm have different beating patterns and swimming trajectories in Newtonian (left) and viscoelastic (right) media. (Ho and Suarez, Reprod. Dom. Anim. 2003.)
Low Reynolds-number swimming in gels
Microorganisms also swim through viscoelastic gels, such as mucus, which are solid rather than fluid. For example, Spirochetes have been observed to swim faster in gels than Newtonian fluids. What does it mean to swim through a solid? The simplest model swimmer is the Taylor sheet, an infinite two dimensional surface with traveling waves. For the Taylor sheet in continuum models of gels, microscopic heterogeneity affects boundary conditions and the elastic phase can lead to enhanced swimming speeds. (preprint)
Image caption: A sheet swimming through a gel. The network density determines whether the swimmer pushes directly against the network (top) or has solvent-mediated interactions with the network.
Nonlinear viscoelastic effects
Even for a fixed, prescribed swimming stroke, nonlinear viscoelasticity affects swimming speeds. In Newtonian fluids, kinematic reversibility in the low Reynolds number limit restricts effective swimming motions to those that do not appear the same going forward and backward in time. Additional swimming motions become available to microorganisms in nonlinearly viscoelastic fluids. (Published in Physics of Fluids [pdf].) Nonlinear effects are also important for swimming in gels.
Image caption: In a nonlinearly viscoelastic fluid the swimming speed depends on the difference between displacement amplitudes of the end spheres.
Finite-length swimmer in a nonlinearly viscoelastic fluid
Finite-size swimmers may behave differently than infinite sheets or cylinders in viscoelastic fluids. Using a boundary-perturbation analysis, we find the swimming speed of the simple Golestanian three-sphere swimmer in an Oldroyd-B fluid. The effect of viscoelasticity depends on swimming stroke asymmetry, a feature not present in infinite swimmers. Can similar methods be used to efficiently investigate swimmers with more complex geometries in viscoelastic fluids? [Funded by NSF CBET-CAREER-1252182]
Image caption: Sperm amongst the mucin fibers comprising the microstructure of cervical mucus. Fiber and mesh sizes are comparable to sperm size. (Ruttlant et al., Reprod. Dom. Anim. 2005)
Swimming through heterogeneous environments
Cervical mucus is made of a network of glycoprotein fibers, and has a microstructure with features on the same scale as the sperm which swim through it. To the sperm, these features appear as random (possibly compliant) obstacles. How are swimmers affected by random media? More generally, swimming in a random environment is relevant not only to swimming in gels, but also to the spread of microbes through soil, fractures, or porous media. [Funded by NSF CBET-CAREER-1252182]
Image caption: H. pylori secretes chemicals to de-gel the surrounding gastric mucus. Image from Bansil et al, National Science Foundation.
Swimming confined by complex media
In complex media, some microorganisms alter the nearby rheology as they swim through. For example, rotating flagella may mechanically deplete polymers nearby in polymeric solutions, while Helicobacter pylori neutralizes stomach acidity in its vicinity, which de-gels nearby gastric mucus. We examine the simplest model of such a scenario by considering a Taylor sheet swimming through a layer of Newtonian fluid bounded by a Brinkman medium. We calculate swimming velocities for constant stroke as well as constant power generation. For the case of H. pylori, by coupling to diffusion we consider how the bacteria self-generates its confined environment and find estimates for the size of the de-gelled “hole” in gastric mucus induced by H pylori.
Image caption: Swimming sheet in a layer of Newtonian fluid bounded by a Brinkman medium.
Visualization of burrowing forces in granular media